AN INVENTORY OF EFFECTIVE STRATEGIES
​FOR VARYING LESSON PURPOSES

This page is an ongoing work-in-progress. Some of the strategies below are simply listed without explanation, for now, and some are explained and have links to resources you can use to better understand them. Rather than wait for the entire page to be completed, we've decided to post it live as we build it. Thanks for bearing with us and we build it out.

Okay, so what are we looking at in the columns below?
Whose research is this? ​How is it organized?

WHAT YOU'RE LOOKING AT (below): This page is split into three columns, organizing effective teaching and learning strategies into 3 categories, based upon the purpose for the lesson in which you are using them.

WHOSE RESEARCH? The research data is organized by effect sizes, based on the work of John Hattie for his series of books titled Visible Learning. In the applied-to-the-classroom books by John Hattie, Douglas Fisher and Nancy Frey (pictured to the left), these three categories are: Surface, Depth, and Transfer, and it should be pointed out that in Hattie & Donoghue's conceptual model of these categories, surface learning and deep learning are split into surface acquisition and surface consolidation, as well as deep acquisition and deep consolidation. ​

WHAT THE EFFECT SIZE NUMBERS MEAN FOR THE STRATEGIES BELOW: In Hattie's Visible Learning compendium of meta-analyses, the larger the effect size, the more effective the approach. Anything at or above 0.4 is considered to be the "Zone of Desired Effects." Hattie argues that it makes sense for teachers and schools to focus their energy on improving skills with these approaches. If you want to learn more about how Hattie calculates his effect sizes, check this page or come down to the office to check out one of Hattie's books (we have them all available for check out) - each of them explains this background.  

HOWEVER, the Big Idea in the Visible Learning books is that it is NOT as simple as looking at the list and learning the top 10 effect size strategies and just using those over and over (probably not a surprise to you at all). Instead, some strategies are most helpful with some lesson learning goals. Where we are in the stage of what students are learning should determine what approaches we use, Hattie and co-authors Fisher and Frey argue. Further, they argue that some strategies whose effect size is below 0.4 in the core research may actually be much more effective when used in a different sequence or stage of learning. They make this case, for example, for inquiry-based learning (0.4 overall) and learning simulations (0.33). They argue that when these strategies follow surface learning and consolidation, they can become powerful deep learning and/or transfer learning strategies (with signs that the effect sizes would be higher if that were the case). 

THE BIG IDEA

"What and when are equally important when it comes to instruction that has an impact on learning. Approaches that facilitate students' surface-level learning do not work equally well for deep learning, and vice versa. Matching the right approach with the appropriate phase of learning is the critical lesson to be learned." - Hattie, Fisher and Frey (Visible Learning for Mathematics, 2017)

SURFACE

"Surface learning does not mean superficial learning. Rather, surface learning is a time when students initially are exposed to concepts, skills, and strategies. Surface learning is critical because it provides a foundation on which to build as students are asked to think more deeply." - Hattie, Fisher and Frey (Visible Learning for Mathematics, 2017)

DEEP

"We define deep learning as a period when students consolidate their understanding and apply and extend some surface learning knowledge to support deeper conceptual understanding . . . We think of this as a 'sweet spot' that will often take up more instructional time, but can be accomplished only when students have the requisite knowledge to go deeper." - Hattie, Fisher and Frey (Visible Learning for Mathematics, 2017)
Nurturing Deep Learning

TRANSFER

"Transfer learning [is] the point at which students take their consolidated knowledge and skills and apply what they know to new scenarios and different contexts. It is also a time when students are able to think metacognitively, reflecting on their own learning and understanding."  - Hattie, Fisher and Frey (Visible Learning for Mathematics, 2017)

SURFACE

Jigsaw method (1.2)

HATTIE: 1.2 effect size
USEFUL FOR: virtually all subjects; can potentially be used for deep learning and transfer learning, as well
SITE: The Jigsaw Classroom 
You're probably familiar with this method, which starts with 4, 5 or 6 students (we prefer 4) each learning a chunk of content. The students then go to expert groups to double check their understanding and make sure they can teach the material to other students. Then they return to their home group and take turns teaching the material. 
The part we often forget is the next one, but it's arguably the crucial part: check every student's understanding of every piece of content (whether with a quiz or other method). The super helpful video summary by Jennifer Gonzalez (Cult of Pedagogy) provided above has some cool ideas about how to combine individual and group score aspects into the quiz / check finale of the Jigsaw lesson. 

​Furthermore, there are many possible extensions. John Hattie, Nancy Frey and Douglas Fisher (writing in Visible Learning for Science; Corwin, 2018) mention a next step in which students return to their expert teams and discuss how the different content components relate to one another (this can be an opportunity for moving from surface to deep learning or transfer learning). Base teams could also take the information learned in expert teams and combine it to solve a problem, apply the knowledge to make something new, or to create an interpretive project. 

Integrating prior knowledge (0.93)

One theme that quickly emerges as you scan across the strategies for teaching at the surface, deep and transfer levels is that determining, activating and integrating prior knowledge is one of the most powerful teaching strategies. While the research is clear on this point, less well-known are the variety of ways we can do this in our classes. The links (and book excerpt recommendations from our lending library) below attempt to tackle that question. 
Edutopia: Are You Tapping Into Prior Knowledge Often Enough in Your Classroom?
8 Strategies to Quickly Assess Prior Knowledge

Summarization (0.79)

Mnemonics (0.76)

Leveraging prior knowledge (0.65)

Vocabulary programs (0.62)

Direct instruction (0.6)

Organizing (0.6)

Recordkeeping (0.52)

Note-taking (0.5)

This post by Jennifer Gonzalez does a great job of summarizing (and citing) much of the latest research on good note-taking practices that can help students to learn more. She helpfully includes a video on ideas for combining Cornell Notes and sketch-noting, and there are plenty of excellent ideas here. 

Imagery (0.45)

DEEP

Organizing and transforming notes (0.85)

While note taking is a key strategy for surface learning (acquisition from reading, video and lecture), going deeper by returning to notes and transforming them adds major power to their value.
CULT OF PEDAGOGY: "Note-Taking: A Research Roundup" (2018)
We re-posted Jennifer Gonzalez's research roundup here because it includes aspects of organizing and transforming notes by going back to them. Check back as we attempt to add more resources and strategies for effectively transforming those notes. 

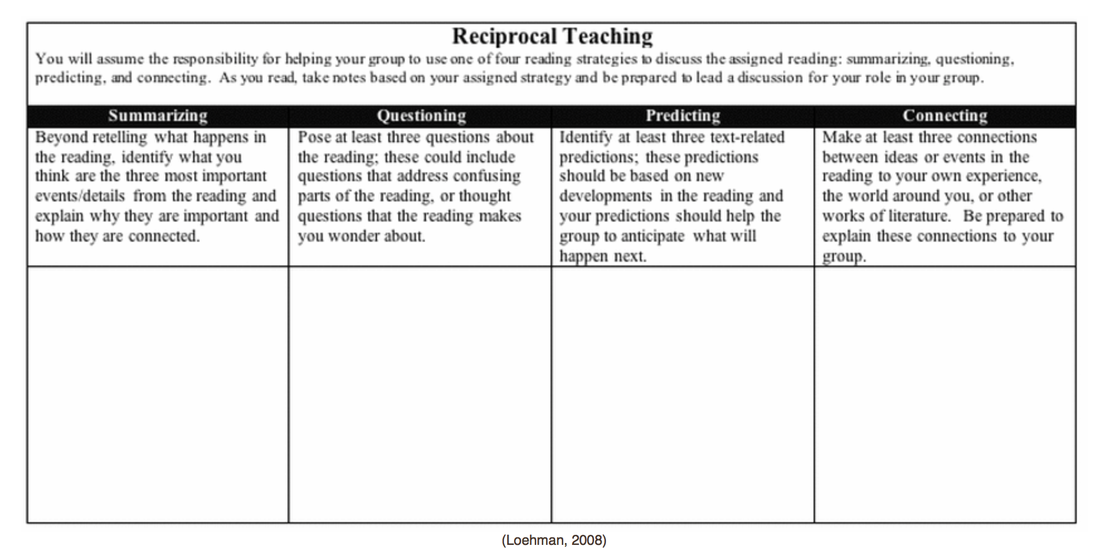
Class discussion (0.82)

Reciprocal teaching (0.74)

HATTIE: 0.74 effect size
USEFUL FOR: Reading comprehension in almost any subject, but can be adapted for Math problem solving (see 3rd video below)
Reciprocal Teaching is a specific strategy that combines cooperative learning, classroom discussion, reading comprehension and metacognitive "learning to learn" approaches (all of which are highly effective approaches). It involves students each participating in one of four different ​specified roles (summarizer, questioner, clarifier, predictor) with each paragraph they read. Thus, it is a collaborative close reading strategy that is ideal for challenging reading material. 
VIDEO EXPLANATION FOR TEACHERS  (click the image immediately below):
Picture
BELOW: A variation in which the 4th student connects ideas from the reading to the world, instead of predicting what is next (other variations include drawing the ideas)
VIDEO EXPLANATION FOR STUDENTS:
USING RECIPROCAL TEACHING WITH MATH PROBLEM SOLVING (example):

Concept mapping (0.64)

Metacognitive strategy instruction (0.6)

Self-questioning (0.55)

Teacher Questioning (0.48)

Inquiry-based teaching (0.4)

Simulations (0.33)

TRANSFER

Identifying underlying similarities & differences (1.32)

Example 1 to 5 assessment of comparison and contrast

Transforming conceptual knowledge (0.85)

Organizing conceptual knowledge (0.85)

Formal discussions (0.82)

Problem-solving teaching (0.68)

Synthesizing information across texts (0.63); reading across documents

Peer tutoring (0.53)

CORE TEACHING FACTORS THAT MAKE A BIG DIFFERENCE

Teacher credibility (0.9)

Spaced (vs. massed) practice (0.6)

Teacher clarity (0.75)

Cooperative learning: compared to individual (0.57); compared to competitive (0.55)

Feedback (0.7)

Teacher-student relationships (0.52)